Collection of Side Work Completed


Preface

      During the process of code development, intermittent problems commonly appear. These problems usually might not have much in common with actual main problem to be solved. These side-quests are part of the journey. This is a collection of things I accomplished.

Index

  1. Iterating Subsets of a Set
    1. Problem
    2. Solution
    3. Example
  2. Map Route within Polygon
    1. Problem
    2. Solution
    3. Example
  3. Indeed Completed Assessments
  4. Fat Line Problem
    1. Problem
    2. Solution
    3. Example




1. Iterating Subsets of a Set #top

a) Problem #top

      While taking a test regarding my C++ skills, a specific subset of a set of elements had to be found. The target subset was defined by a list of criteria. The number of subsets of a specific size is given by the formula of combinations:
nCr = n! / ( r! * (n - r)!) where n=set_size and r=subset_size
The goal is to iterate all combinations of all sizes while keeping in mind the cardinality. I knew this was more of a academic problem, because the set can only have a relatively small cardinality e.g.: the set of all subsets (including itself and the null set) of a set of size 20 has a size of more then a million.

b) Solution #top

      The number of all subsets of a set (size=n) is giving by 2n. The way this works is: every independent element of the set is either active or not → base_twoset_size. This then allows to iterate subsets by converting the iterant integer to a binary number and pad it from the front with zeros and use it as an activation vector.

c) Example #top

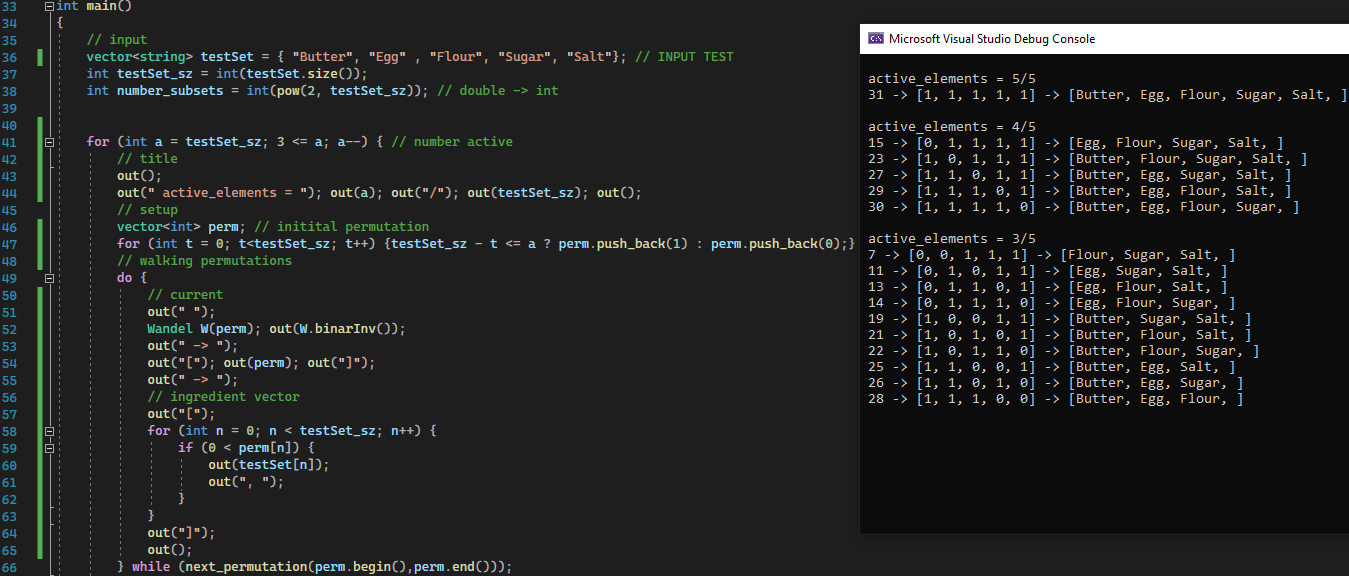
Programmed in C++ using classes: <vector>, <algorithm>, and my own class "Wandel".
input: testSet = {"Butter", "Egg" , "Flour", "Sugar", "Salt"};
We can say that we need at least three ingredients to search for a recipe. Giving what we have as inventory, we can walk combinations in such a way that we make the most of what is in the fridge. This is an approach of optimization.

cPlusPlusSubset



2. Map Route within Polygon #top

a) Problem #top

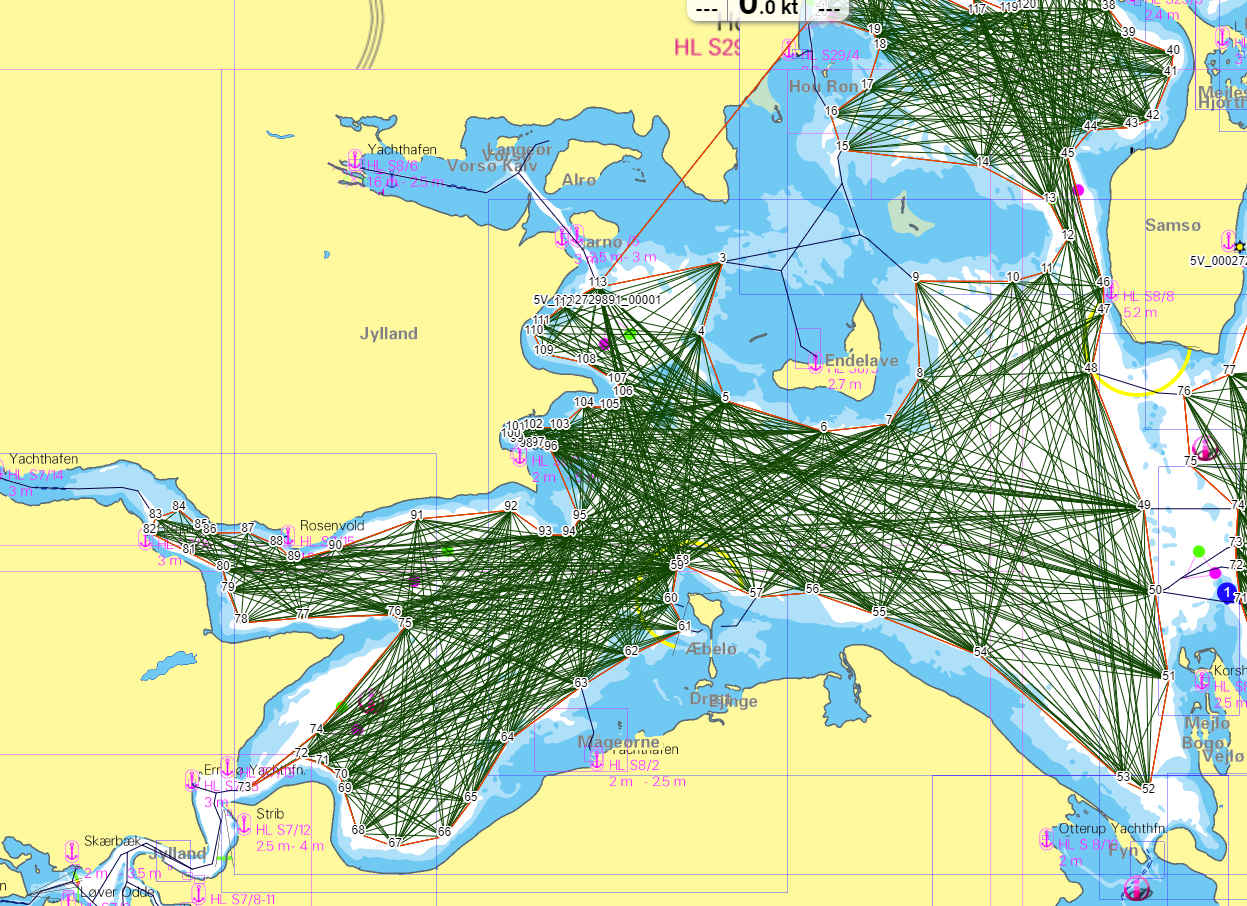
      Given: A list of finite points, size=c, in a (cartesian) R2 space. The points provided are sequential, and form a single (possible concave) polygon: {P0,P1, … , Pc-1}. The goal was to find all, finite non-zero length, line segments from any two points of the polygon such that they are completely within the polygon.

b) Solution #top

      Given m,n,t ∈ W (the set of whole numbers: {0,1,2,...}), such that Pm, Pn, Pt ∈ P (points of perimeter of polygon). Then the line from Pm to Pn, denoted by L(Pm, Pn) lies completely within the polygon area, A, if and only if all intersections of L(Pm, Pn) and all polygon line segments do not intersect (within segment range). Coded in C++.

c) Example #top

      The goal here was to visualize all possible routs (lines) within the large concave polygon from one node to another.

mapRoute




3. Indeed Completed Assessments #top

assessments_indeed.png




4. Fat Line Problem #top

a) Problem #top

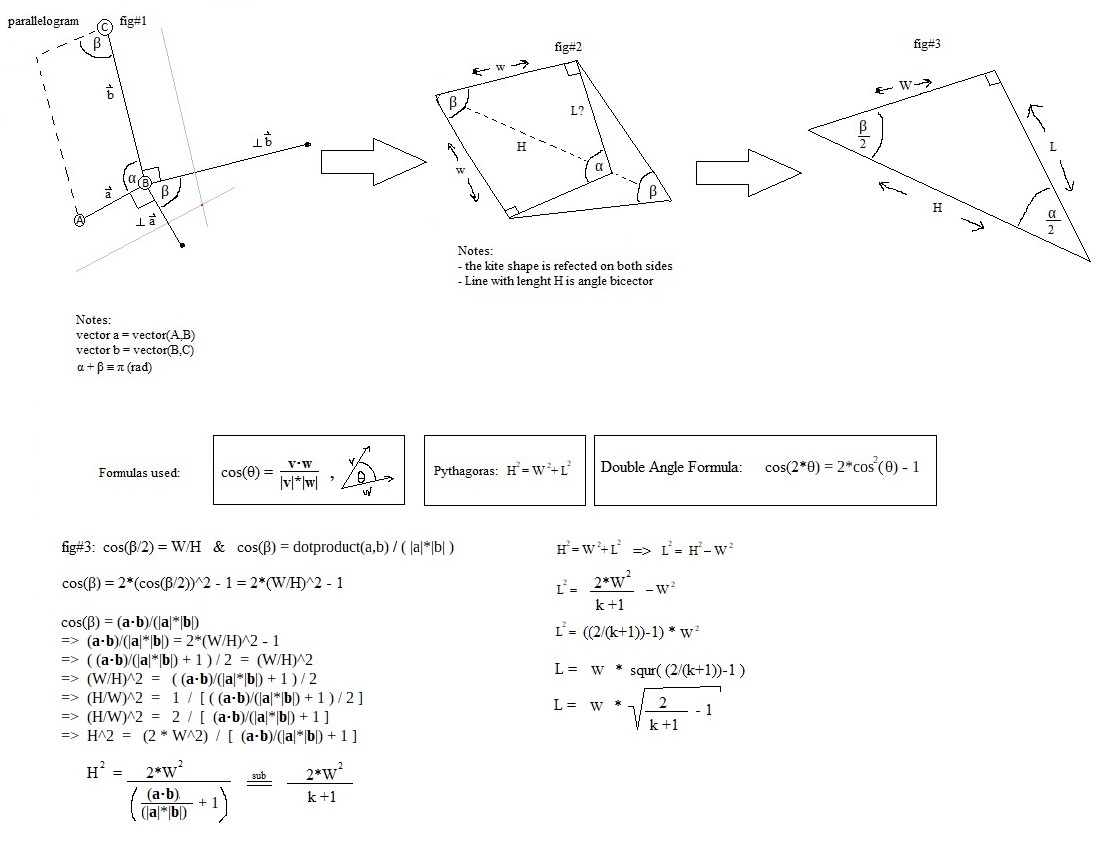
      The fat line problem consists of the following lemma algorithm: You have two points in the standard xy-plain or more formally known as cartesian R2. You want to join these points with a line and are able to calculate which pixels to color in with a given line-radius of r. But what do you do when three sequential points have an angle and you have to compute fast?
Below you can see the problem in a HTML Canvas element:

b) Solution #top

      I wrote a more formatted proof later, but this was my pen and paper initial draft.

FatLine-Proof

c) Example #top

      This is the formula shown in action in MS Excel.

fatLineExample.png




#top
© Copyright 2021, Henrik Singendonk